MR. LUPINACCI'S CLASSROOM
Honors Geometry p. 191 #10, 12, 13, 14, 16
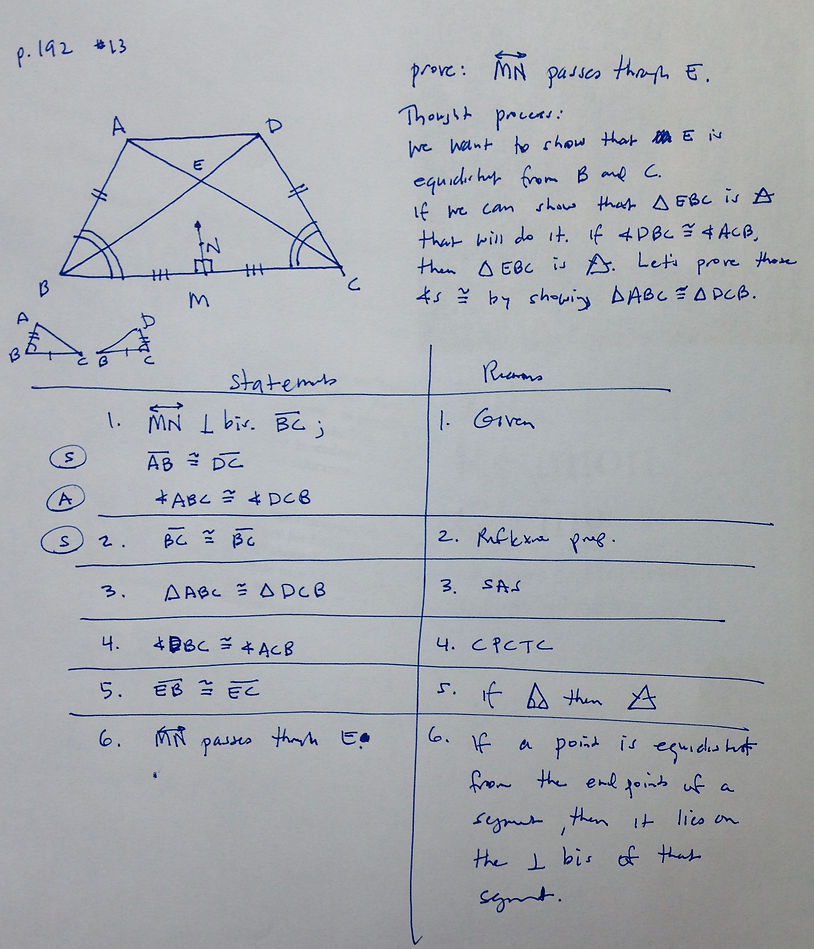
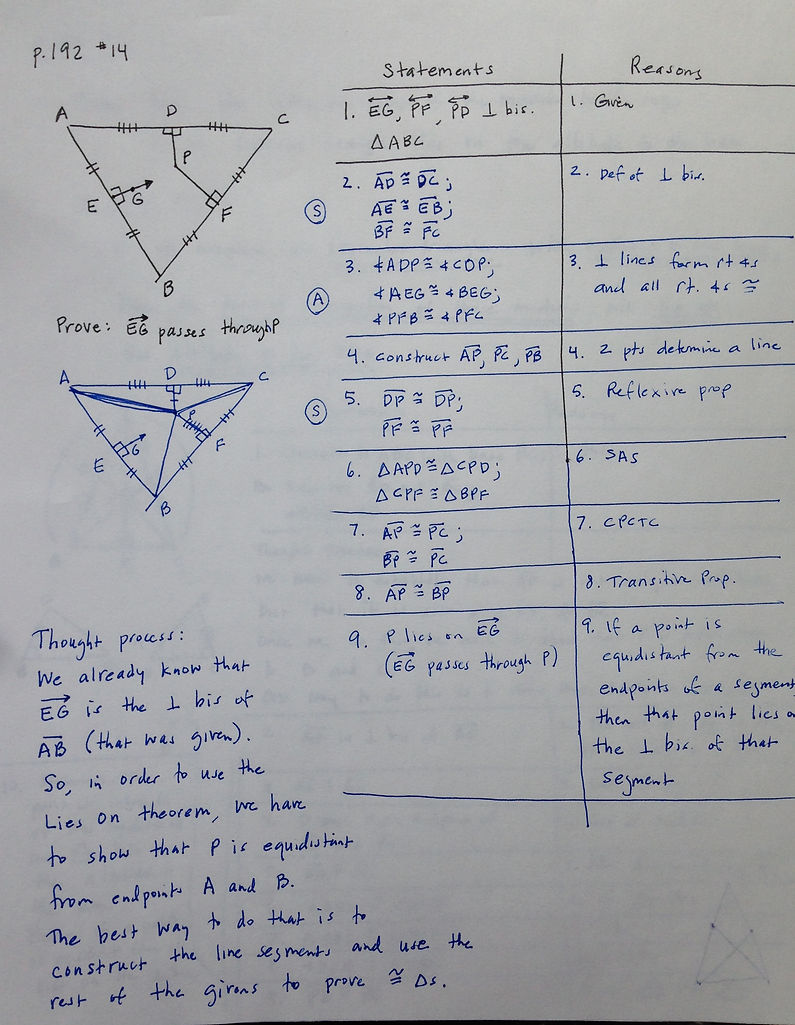
Now we're proving some LIES ON Theorem problems - yes! This is some great stuff.
As with the previous proofs we've discussed, we want to FORMULATE A STRATEGY that connects the TO PROVE with THE GIVEN:
TO PROVE <-------------- STRATEGY -----------------> THE GIVEN
So focus on what you're trying TO PROVE, then WORK BACKWARDS to develop a STRATEGY and then explore your options based on THE GIVEN in order to decide on your final PLAN OF ACTION. (This may require drawing some separate congruent triangles, etc.)
With that being said, we have some additional advice from our friend Blocky, who tells us a very STRICT PROCEDURE on how to solve these proofs, on p, 187. If you're not sure what that says, DEFINITELY review his/her advice first.
I've included some of my own notes on some of these proofs, so if you're stuck you may want to read what I wrote first and then take another crack at solving the proof before you look my solution.

If you get stuck on #14, read this first: We already know that Ray EG is the perpendicular bisector of AB (that was given). Now, in order to use the LIES ON Theorem, we have to show that P is equidistant from A and B.
So, maybe we need to construct some line segments?
Try constructing some line segments first, and then see if you can develop a strategy to prove PA = PB.
If you're still stuck after giving it a try, then you can look at my solution.
WAIT!!!!
